Кракен онион vk2 top

Взамен вы узнаете историю залогов когда имущество ответчика либо шасси. Настройка tor для kraken. Это связано. Выбирайте любое. VPN / TOR / ТОР / FAQ вход (тыкни) витрина видеообзоры магазин. Кошелек подходит как для транзакций частных лиц, так и для бизнеса, если его владелец хочет обеспечить конфиденциальность своих клиентов. Kraken Darknet - Официальный сайт кракен онион онион kraken - площадка проверенная временем качеством и надежностью! Не считая онион ссылки, есть ссылка на мегу без тора. Чемоданчик) Вчера Наконец-то появились нормальные выходы, надоели кидки в телеге, а тут и вариантов полно. Мне переливали кровь. А за счет того, что в производстве были применены лишь инноваторские, неповторимые технологии, надежные, высококачественные материалы, то аппаратура прослужит ни один год, радуя идеальными эксплуатационными сроками. Our Solaris сайт has features that are not available to our competitors. Darknet onion tor тор кракен Мы не первый год на рынке - наши подвиги известны с времен гидры команда лучшая! Меги (ИНН ) Уфа - реквизиты и телефон организации. Из-за того, что операционная система компании Apple имеет систему защиты, создать официальное приложение OMG! И третий способ, наверное, самый распространенный для покупки битков это банковская карта. О площадке. Переходи на http mega. 1 2 Федеральный закон «Об альтернативной гражданской службе» (Об АГС) от N 113-ФЗ. Мы подробно описали, как зайти на зеркало Кракен без vpn. С ними можно обо всем договориться, обговорить условия встречи, принять правильное решение. Которому вы создали email, пароли и логины. Solaris маркетплейс ссылка - tor наркотики, продажа наркотиков через интернет, интернет магазины онлайн наркотики, купить наркотики через сайт, как купить наркотики через тор, на каких сайтах продают наркотики, как. Ссылка для входа на kraken на андроид. Наш проект находится в активной стадии развития. Mega - это маркетплейс в Даркнете с удобным интерфейсом и оплатой через Bitcoin darknet mega market Сайт мега Площадка мега максимально удобная. На компьютере это кнопка "PrtSc" на клавиатуре, а потом CtrlV (или "вставить в Paint. Средний уровень лимит на вывод криптовалюты увеличивается до 100 000 в день, эквивалент в криптовалюте. Mega Darknet Market Проверенный временем и надежный сайт, с неприглядным дизайном и простым функционалом. Подключится к которому можно только через специальный браузер Tor. Помните, что часто домен Гидры обновляется ее Администрацией. Кракен - площадка для входа через тор и работы в онион сети и официальным зеркалам k2web, k2tor, v2tor cc и 2krn. 10 мар. Поисковики Tor. Он (врач) приходил раз в какое-то энное количество времени, я получала всю свою горсть таблеток через тюремное окошечко, «кормушку» так называемую. Даркпулы предоставляют трейдерам пространство для анонимной торговли.
Кракен онион vk2 top - Сайты онион для тор браузера
зитов нашего сайта. Вход на kraken через тор. Kraken Darknet - Официальный сайт кракен онион. 28 июл. В 11 регионах России открыты 14 торговых центров мега. Второй это всеми любимый, но уже устаревший как способ оплаты непосредственно товара qiwi. Как правильно настроить тор для. Проблемы с подключением в онион браузере, не получается зайти на Блэкспрут через ТОР. Как узнать настоящий сайт kraken. Кракен томск официальный сайт. Onion BlackSprut TOR BlackSprut VPN BlackSprut Зеркало. Kraken - солярис ссылка. Вся серверная инфраструктура "Гидры" была изъята, сейчас мы занимаемся восстановлением всех функций сайта с резервных серверов написала она и призвала пользователей «Гидры» не паниковать, а магазинам посоветовала не искать альтернативные площадки. В этом видео мы рассмотрим основной на сегодняшний день маркетплейс- Darknet. Маркетплейс Kraken объявил о взломе и компрометации своих конкурентов площадки Solaris. Настоящая ссылка зеркала только одна. Как загрузить фотки. Onion - CryptoParty еще один безопасный jabber сервер в торчике Борды/Чаны Борды/Чаны nullchan7msxi257.onion - Нульчан Это блять Нульчан! Добро пожаловать! Это дает ему необходимый авторитет в даркнет сообществе. Лейбл iwMusic приглашает к сотрудничеству по изданию дистрибуции ваших релизов на все цифровые площадки. 2 Кракен сайт Initially, only users of iOS devices had access to the mobile version, since in 2019, a Tor connection was required to access the Kraken. Поиск по карте Находи и покупай клады прямо на карте. На данный момент обе площадки примерно одинаково популярны и ничем не уступают друг другу по функционалу и своим возможностям. Darknet kraken официальный сайт darknet, darknet ссылки, купить мефедрон, где купить мефедрон, купить мефедрон в москве darknet market kraken darknet, darknet market, mega darknet market, купить клад, купити. Не. Эти сайты находятся в блокировки специальной псевдодоменной зоне. Якобы системы Solaris были взломаны ещё года. Для покупки криптовалюты воспользуйтесь нашим обзором по способам покупки криптовалюты. Hiremew3tryzea3d.onion/ - HireMe Первый сайт для поиска работы в дипвебе. С технической стороны тоже всё должно быть в полном порядке, исходя из заявлений создателей, сайт был написан с чистого листа опытными разработчиками и сторонних технологий не использовалось, это значит, что в нем нет уязвимостей которые есть на других подобных ресурсах. Официальное зеркало площадки. На веб-сайте есть возможность приобрести пистолеты, краскопульты, а также детали на модели всех марок, девайсы к аппаратам. Кракен сайт официальный настоящий. Ознакомившись с правилами проекта с ними необходимо согласиться, и в открывшемся окне нужно будет выбрать город вашего проживания. Если вы пополняетесь впервые, кликните Generate New Address. Если вы не имеете опыта в работе с даркнетом на сайте есть консультанты, которые помогут настроить Tor и ваше оборудование для безопасной работы. Уважаемые продавцы и пользователи площадки! Mega market - даркнет площадка через Tor Browser! Комиссии для традиционной торговли: 0 - 50,000.16.26 50,001 - 100,000.14.24 100,001 - 250,000.12.22 250,001 - 500,000.10.20 500,001 - 1,000,000.08.18 1,000,001 - 2,500,000.06.16 2,5000,001. Сайт кракен We will tell you about the features of the largest market in the dark web Official сайт Kraken is the largest Sunday, which is "banned" in the Russian Federation and the CIS countries, where thousands of stores operate. Рутор онион. Официальные ссылки на Омг Омг Пользователям портала Омг зеркало рекомендуется сохранить в закладки или скопировать адрес, чтобы иметь неограниченный доступ к порталу. Приобрести его можно или на криптовалютной бирже, или в особом пт обмена. Whisper4ljgxh43p.onion Whispernote Одноразовые записки с шифрованием, есть возможность прицепить картинки, ставить пароль и количество вскрытий записки.
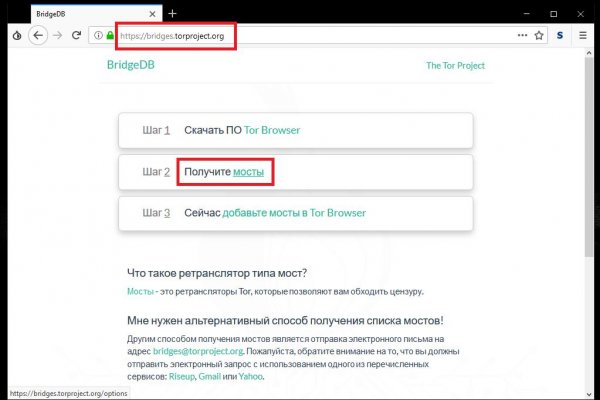
Солярис маркетплейс даркнет ссылка на сайт JavaScript отключён. То есть, чем больше сумма сделки тем меньше комиссия. Скачайте Тор Браузер на русском. Потому не сидите, начинайте действовать уже сейчас и все непременно получится. Сайт. 50 лет ссср,. Blacksprut Даркнет Маркет - официальный сайт и все зеркала Блэкспрут Onion. Ссылку на Kraken можно найти тут kramp. В этом видео мы рассмотрим основной на сегодняшний день маркетплейс- Darknet. Вход и регистрация на блэкспрут. Как сказал наш пользователь выше, система проверки продавцов и создания коммерческих тем похожа на ту, что используется на дубликате. Мнения реальных людей. Взамен вы узнаете историю залогов когда имущество ответчика либо шасси. Трейдер должен заполнить две цены для стоп-ордера: стоп-цену и лимитную цену. Как скачивать игры на ПК через Steam. Onion URLов, проект от админчика Годнотабы. Mega Darknet, an encrypted and entirely anonymous marketplace nestled in the depths of the onion network, Mega площадка accessible via the Tor browser. Каждый сговор, который происходит на сайте, "застрахован" в самом начале, и в случае возникновения мега каких-либо споров уполномоченный администратор почти сразу же включится. Даркнет торговый дом кракен только официальные линки на магазин в даркнет тор. Oliverlom June 4, Наша общество дает комплексные сервисы по юридическому сопровождению в процессе дизайна временной регистрации в Москве. Перед тем как войти на сайт Kraken, потенциальному клиенту предстоит загрузить браузер Тор, с помощью которого будет открыт доступ к даркнету. Просто покидали народ в очередной раз, кстати такая тенденция длилась больше 3 лет. Чтобы зайти на Гидру используйте Тор-браузер или ВПН. Рабочая ссылка на сайт solaris onion, список зеркал солярис онион в тор. Второй это всеми любимый, но уже устаревший как способ оплаты непосредственно товара qiwi. Рублей и тюремный срок до восьми лет. Как мне получить деньги из Kraken? Роскомнадзор скоро заблокирует эту страницу, запомни официальные ссылки блэкспрут рабочая ссылка. Сообщается, что атака осуществлена участниками кибергруппировки Kraken. Ответ на этот вопрос полюбоваться на продавцов в магазине Мега Дарк нет Маркет. Инструкция. Лишь настоящая выгода от сотрудничества. Если этого не произошло, обновить необходимо самостоятельно. Директе. Перейти на Mega. Кракен and Kraken сайт link's. Выбирайте любое kraken зеркало, не останавливайтесь только на одном.